GF Logo

Grammatical Framework Tutorial

Aarne Ranta

December 2010 for GF 3.2

Overview

This is a hands-on introduction to grammar writing in GF.

Main ingredients of GF:

Prerequisites:

Outline

Lesson 1: a multilingual "Hello World" grammar. English, Finnish, Italian.

Lesson 2: a larger grammar for the domain of food. English and Italian.

Lesson 3: parameters - morphology and agreement.

Lesson 4: using the resource grammar library.

Lesson 5: semantics - dependent types, variable bindings, and semantic definitions.

Lesson 6: implementing formal languages.

Lesson 7: embedded grammar applications.

Lesson 1: Getting Started with GF

Goals:

What GF is

We use the term GF for three different things:

The GF system is an implementation of the GF programming language, which in turn is built on the ideas of the GF theory.

The focus of this tutorial is on using the GF programming language.

At the same time, we learn the way of thinking in the GF theory.

We make the grammars run on a computer by using the GF system.

GF grammars and language processing tasks

A GF program is called a grammar.

A grammar defines a language.

From this definition, language processing components can be derived:

In general, a GF grammar is multilingual:

Getting the GF system

Open-source free software, downloaded via the GF Homepage:

grammaticalframework.org

There you find

Many examples in this tutorial are online.

Normally you don't have to compile GF yourself. But, if you do want to compile GF from source follow the instructions in the Developers Guide.

Running the GF system

Type gf in the Unix (or Cygwin) shell:

    % gf

You will see GF's welcome message and the prompt >. The command

    > help

will give you a list of available commands.

As a common convention, we will use

Thus you should not type these prompts, but only the characters that follow them.

A "Hello World" grammar

Like most programming language tutorials, we start with a program that prints "Hello World" on the terminal.

Extra features:

The program: abstract syntax and concrete syntaxes

A GF program, in general, is a multilingual grammar. Its main parts are

The abstract syntax defines what meanings can be expressed in the grammar

GF code for the abstract syntax:

    -- a "Hello World" grammar
    abstract Hello = {
  
      flags startcat = Greeting ;
  
      cat Greeting ; Recipient ;
  
      fun
        Hello : Recipient -> Greeting ;
        World, Mum, Friends : Recipient ;
    }

The code has the following parts:

English concrete syntax (mapping from meanings to strings):

    concrete HelloEng of Hello = {
  
      lincat Greeting, Recipient = {s : Str} ;
  
      lin
        Hello recip = {s = "hello" ++ recip.s} ;
        World = {s = "world"} ;
        Mum = {s = "mum"} ;
        Friends = {s = "friends"} ;
    }

The major parts of this code are:

Notice the concatenation ++ and the record projection ..

Finnish and an Italian concrete syntaxes:

    concrete HelloFin of Hello = {
      lincat Greeting, Recipient = {s : Str} ;
      lin
        Hello recip = {s = "terve" ++ recip.s} ;
        World = {s = "maailma"} ;
        Mum = {s = "äiti"} ;
        Friends = {s = "ystävät"} ;
    }
  
    concrete HelloIta of Hello = {
      lincat Greeting, Recipient = {s : Str} ;
      lin
        Hello recip = {s = "ciao" ++ recip.s} ;
        World = {s = "mondo"} ;
        Mum = {s = "mamma"} ;
        Friends = {s = "amici"} ;
    }

Using grammars in the GF system

In order to compile the grammar in GF, we create four files, one for each module, named Modulename.gf:

    Hello.gf  HelloEng.gf  HelloFin.gf  HelloIta.gf

The first GF command: import a grammar.

    > import HelloEng.gf

All commands also have short names; here:

    > i HelloEng.gf

The GF system will compile your grammar into an internal representation and show the CPU time was consumed, followed by a new prompt:

    > i HelloEng.gf
    - compiling Hello.gf...   wrote file Hello.gfo 8 msec
    - compiling HelloEng.gf...   wrote file HelloEng.gfo 12 msec
  
    12 msec
    >

You can use GF for parsing (parse = p)

    > parse "hello world"
    Hello World

Parsing takes a string into an abstract syntax tree.

The notation for trees is that of function application:

    function argument1 ... argumentn

Parentheses are only needed for grouping.

Parsing something that is not in grammar will fail:

    > parse "hello dad"
    The parser failed at token 2: "dad"
  
    > parse "world hello"
    no tree found

You can also use GF for linearization (linearize = l). It takes trees into strings:

    > linearize Hello World
    hello world

Translation: pipe linearization to parsing:

    > import HelloEng.gf
    > import HelloIta.gf
  
    > parse -lang=HelloEng "hello mum" | linearize -lang=HelloIta
    ciao mamma

Default of the language flag (-lang): the last-imported concrete syntax.

Multilingual generation:

    > parse -lang=HelloEng "hello friends" | linearize
    terve ystävät
    ciao amici
    hello friends

Linearization is by default to all available languages.

Exercises on the Hello World grammar

  1. Test the parsing and translation examples shown above, as well as some other examples, in different combinations of languages.

  2. Extend the grammar Hello.gf and some of the concrete syntaxes by five new recipients and one new greeting form.

  3. Add a concrete syntax for some other languages you might know.

  4. Add a pair of greetings that are expressed in one and the same way in one language and in two different ways in another. For instance, good morning and good afternoon in English are both expressed as buongiorno in Italian. Test what happens when you translate buongiorno to English in GF.

  5. Inject errors in the Hello grammars, for example, leave out some line, omit a variable in a lin rule, or change the name in one occurrence of a variable. Inspect the error messages generated by GF.

Using grammars from outside GF

You can use the gf program in a Unix pipe.

    % echo "l Hello World" | gf HelloEng.gf HelloFin.gf HelloIta.gf

You can also write a script, a file containing the lines

    import HelloEng.gf
    import HelloFin.gf
    import HelloIta.gf
    linearize Hello World

GF scripts

If we name this script hello.gfs, we can do

    $ gf --run <hello.gfs
  
    ciao mondo
    terve maailma
    hello world

The option --run removes prompts, CPU time, and other messages.

See Lesson 7, for stand-alone programs that don't need the GF system to run.

Exercise. (For Unix hackers.) Write a GF application that reads an English string from the standard input and writes an Italian translation to the output.

What else can be done with the grammar

Some more functions that will be covered:

Embedded grammar applications

Application programs, using techniques from Lesson 7:

Lesson 2: Designing a grammar for complex phrases

Goals:

The abstract syntax Food

Phrases usable for speaking about food:

Abstract syntax:

    abstract Food = {
  
      flags startcat = Phrase ;
  
      cat
        Phrase ; Item ; Kind ; Quality ;
  
      fun
        Is : Item -> Quality -> Phrase ;
        This, That : Kind -> Item ;
        QKind : Quality -> Kind -> Kind ;
        Wine, Cheese, Fish : Kind ;
        Very : Quality -> Quality ;
        Fresh, Warm, Italian, Expensive, Delicious, Boring : Quality ;
    }

Example Phrase

    Is (This (QKind Delicious (QKind Italian Wine))) (Very (Very Expensive))
    this delicious Italian wine is very very expensive

The concrete syntax FoodEng

    concrete FoodEng of Food = {
  
      lincat
        Phrase, Item, Kind, Quality = {s : Str} ;
  
      lin
        Is item quality = {s = item.s ++ "is" ++ quality.s} ;
        This kind = {s = "this" ++ kind.s} ;
        That kind = {s = "that" ++ kind.s} ;
        QKind quality kind = {s = quality.s ++ kind.s} ;
        Wine = {s = "wine"} ;
        Cheese = {s = "cheese"} ;
        Fish = {s = "fish"} ;
        Very quality = {s = "very" ++ quality.s} ;
        Fresh = {s = "fresh"} ;
        Warm = {s = "warm"} ;
        Italian = {s = "Italian"} ;
        Expensive = {s = "expensive"} ;
        Delicious = {s = "delicious"} ;
        Boring = {s = "boring"} ;
    }

Test the grammar for parsing:

    > import FoodEng.gf
    > parse "this delicious wine is very very Italian"
    Is (This (QKind Delicious Wine)) (Very (Very Italian))

Parse in other categories setting the cat flag:

    p -cat=Kind "very Italian wine"
    QKind (Very Italian) Wine

Exercises on the Food grammar

  1. Extend the Food grammar by ten new food kinds and qualities, and run the parser with new kinds of examples.

  2. Add a rule that enables question phrases of the form is this cheese Italian.

  3. Enable the optional prefixing of phrases with the words "excuse me but". Do this in such a way that the prefix can occur at most once.

Commands for testing grammars

Generating trees and strings

Random generation (generate_random = gr): build build a random tree in accordance with an abstract syntax:

    > generate_random
    Is (This (QKind Italian Fish)) Fresh

By using a pipe, random generation can be fed into linearization:

    > generate_random | linearize
    this Italian fish is fresh

Use the number flag to generate several trees:

    > gr -number=4 | l
    that wine is boring
    that fresh cheese is fresh
    that cheese is very boring
    this cheese is Italian

To generate all phrases that a grammar can produce, use generate_trees = gt.

    > generate_trees | l
    that cheese is very Italian
    that cheese is very boring
    that cheese is very delicious
    ...
    this wine is fresh
    this wine is warm

The default depth is 3; the depth can be set by using the depth flag:

    > generate_trees -depth=2 | l

What options a command has can be seen by the help = h command:

    > help gr
    > help gt

Exercises on generation

  1. If the command gt generated all trees in your grammar, it would never terminate. Why?

  2. Measure how many trees the grammar gives with depths 4 and 5, respectively. Hint. You can use the Unix word count command wc to count lines.

More on pipes: tracing

Put the tracing option -tr to each command whose output you want to see:

    > gr -tr | l -tr | p
  
    Is (This Cheese) Boring
    this cheese is boring
    Is (This Cheese) Boring

Useful for test purposes: the pipe above can show if a grammar is ambiguous, i.e. contains strings that can be parsed in more than one way.

Exercise. Extend the Food grammar so that it produces ambiguous strings, and try out the ambiguity test.

Writing and reading files

To save the outputs into a file, pipe it to the write_file = wf command,

    > gr -number=10 | linearize | write_file -file=exx.tmp

To read a file to GF, use the read_file = rf command,

    > read_file -file=exx.tmp -lines | parse

The flag -lines tells GF to read each line of the file separately.

Files with examples can be used for regression testing of grammars - the most systematic way to do this is by treebanks; see here.

Visualizing trees

Parentheses give a linear representation of trees, useful for the computer.

Human eye may prefer to see a visualization: visualize_tree = vt:

    > parse "this delicious cheese is very Italian" | visualize_tree

The tree is generated in postscript (.ps) file. The -view option is used for telling what command to use to view the file.

This works on Mac OS X:

    > parse "this delicious cheese is very Italian" | visualize_tree -view=open

On Linux, one can use one of the following commands.

    > parse "this delicious cheese is very Italian" | visualize_tree -view=eog
    > parse "this delicious cheese is very Italian" | visualize_tree -view=xdg-open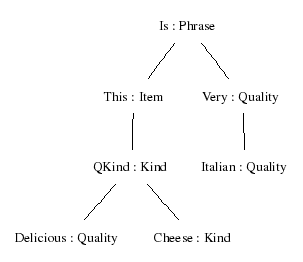

This command uses the program Graphviz, which you might not have, but which are freely available on the web.

You can save the temporary file _grph.dot, which the command vt produces.

Then you can process this file with the dot program (from the Graphviz package).

    % dot -Tpng _grph.dot > mytree.png

You can also visualize parse trees, which show categories and words instead of function symbols. The command is visualize_parse = vp:

    > parse "this delicious cheese is very Italian" | visualize_parse

System commands

You can give a system command without leaving GF: ! followed by a Unix command,

    > ! dot -Tpng grphtmp.dot > mytree.png
    > ! open mytree.png

A system command may also receive its argument from a GF pipes. It then uses the symbol ?:

    > generate_trees -depth=4 | ? wc -l

This command example returns the number of generated trees.

Exercise. Measure how many trees the grammar FoodEng gives with depths 4 and 5, respectively. Use the Unix word count command wc to count lines, and a system pipe from a GF command into a Unix command.

An Italian concrete syntax

Just (?) replace English words with their dictionary equivalents:

    concrete FoodIta of Food = {
  
      lincat
        Phrase, Item, Kind, Quality = {s : Str} ;
  
      lin
        Is item quality = {s = item.s ++ "è" ++ quality.s} ;
        This kind = {s = "questo" ++ kind.s} ;
        That kind = {s = "quel" ++ kind.s} ;
        QKind quality kind = {s = kind.s ++ quality.s} ;
        Wine = {s = "vino"} ;
        Cheese = {s = "formaggio"} ;
        Fish = {s = "pesce"} ;
        Very quality = {s = "molto" ++ quality.s} ;
        Fresh = {s = "fresco"} ;
        Warm = {s = "caldo"} ;
        Italian = {s = "italiano"} ;
        Expensive = {s = "caro"} ;
        Delicious = {s = "delizioso"} ;
        Boring = {s = "noioso"} ;
    }

Not just replacing words:

The order of a quality and the kind it modifies is changed in

      QKind quality kind = {s = kind.s ++ quality.s} ;

Thus Italian says vino italiano for Italian wine.

(Some Italian adjectives are put before the noun. This distinction can be controlled by parameters, which are introduced in Lesson 3.)

Multilingual grammars have yet another visualization option: word alignment, which shows what words correspond to each other. Technically, this means words that have the same smallest spanning subtrees in abstract syntax. The command is align_words = aw:

    > parse "this delicious cheese is very Italian" | align_words

Exercises on multilinguality

  1. Write a concrete syntax of Food for some other language. You will probably end up with grammatically incorrect linearizations - but don't worry about this yet.

  2. If you have written Food for German, Swedish, or some other language, test with random or exhaustive generation what constructs come out incorrect, and prepare a list of those ones that cannot be helped with the currently available fragment of GF. You can return to your list after having worked out Lesson 3.

Free variation

Semantically indistinguishable ways of expressing a thing.

The variants construct of GF expresses free variation. For example,

    lin Delicious = {s = "delicious" | "exquisit" | "tasty"} ;

By default, the linearize command shows only the first variant from such lists; to see them all, use the option -all:

    > p "this exquisit wine is delicious" | l -all
    this delicious wine is delicious
    this delicious wine is exquisit
    ...

An equivalent notation for variants is

    lin Delicious = {s = variants {"delicious" ; "exquisit" ; "tasty"}} ;

This notation also allows the limiting case: an empty variant list,

    variants {}

It can be used e.g. if a word lacks a certain inflection form.

Free variation works for all types in concrete syntax; all terms in a variant list must be of the same type.

More application of multilingual grammars

Multilingual treebanks

Multilingual treebank: a set of trees with their linearizations in different languages:

    > gr -number=2 | l -treebank
  
    Is (That Cheese) (Very Boring)
    quel formaggio è molto noioso
    that cheese is very boring
  
    Is (That Cheese) Fresh
    quel formaggio è fresco
    that cheese is fresh

Translation quiz

translation_quiz = tq: generate random sentences, display them in one language, and check the user's answer given in another language.

    > translation_quiz -from=FoodEng -to=FoodIta
  
    Welcome to GF Translation Quiz.
    The quiz is over when you have done at least 10 examples
    with at least 75 % success.
    You can interrupt the quiz by entering a line consisting of a dot ('.').
  
    this fish is warm
    questo pesce è caldo
    > Yes.
    Score 1/1
  
    this cheese is Italian
    questo formaggio è noioso
    > No, not questo formaggio è noioso, but
    questo formaggio è italiano
  
    Score 1/2
    this fish is expensive

Context-free grammars and GF

The "cf" grammar format

The grammar FoodEng can be written in a BNF format as follows:

    Is.        Phrase  ::= Item "is" Quality ;
    That.      Item    ::= "that" Kind ;
    This.      Item    ::= "this" Kind ;
    QKind.     Kind    ::= Quality Kind ;
    Cheese.    Kind    ::= "cheese" ;
    Fish.      Kind    ::= "fish" ;
    Wine.      Kind    ::= "wine" ;
    Italian.   Quality ::= "Italian" ;
    Boring.    Quality ::= "boring" ;
    Delicious. Quality ::= "delicious" ;
    Expensive. Quality ::= "expensive" ;
    Fresh.     Quality ::= "fresh" ;
    Very.      Quality ::= "very" Quality ;
    Warm.      Quality ::= "warm" ;

GF can convert BNF grammars into GF. BNF files are recognized by the file name suffix .cf (for context-free):

    > import food.cf

The compiler creates separate abstract and concrete modules internally.

Restrictions of context-free grammars

Separating concrete and abstract syntax allows three deviations from context-free grammar:

Exercise. Define the non-context-free copy language {x x | x <- (a|b)*} in GF.

Modules and files

GF uses suffixes to recognize different file formats:

Importing generates target from source:

    > i FoodEng.gf
    - compiling Food.gf...   wrote file Food.gfo 16 msec
    - compiling FoodEng.gf...   wrote file FoodEng.gfo 20 msec

The .gfo format (="GF Object") is precompiled GF, which is faster to load than source GF (.gf).

When reading a module, GF decides whether to use an existing .gfo file or to generate a new one, by looking at modification times.

Exercise. What happens when you import FoodEng.gf for a second time? Try this in different situations:

Using operations and resource modules

Operation definitions

The golden rule of functional programmin:

Whenever you find yourself programming by copy-and-paste, write a function instead.

Functions in concrete syntax are defined using the keyword oper (for operation), distinct from fun for the sake of clarity.

Example:

    oper ss : Str -> {s : Str} = \x -> {s = x} ;

The operation can be applied to an argument, and GF will compute the value:

    ss "boy" ===> {s = "boy"}

The symbol ===> will be used for computation.

Notice the lambda abstraction form

This is read:

For lambda abstraction with multiple arguments, we have the shorthand

    \x,y -> t   ===  \x -> \y -> t

Linearization rules actually use syntactic sugar for abstraction:

    lin f x = t   ===  lin f = \x -> t

The ``resource`` module type

The resource module type is used to package oper definitions into reusable resources.

    resource StringOper = {
      oper
        SS : Type = {s : Str} ;
        ss : Str -> SS = \x -> {s = x} ;
        cc : SS -> SS -> SS = \x,y -> ss (x.s ++ y.s) ;
        prefix : Str -> SS -> SS = \p,x -> ss (p ++ x.s) ;
    }

Opening a resource

Any number of resource modules can be opened in a concrete syntax.

    concrete FoodEng of Food = open StringOper in {
  
      lincat
        S, Item, Kind, Quality = SS ;
  
      lin
        Is item quality = cc item (prefix "is" quality) ;
        This k = prefix "this" k ;
        That k = prefix "that" k ;
        QKind k q = cc k q ;
        Wine = ss "wine" ;
        Cheese = ss "cheese" ;
        Fish = ss "fish" ;
        Very = prefix "very" ;
        Fresh = ss "fresh" ;
        Warm = ss "warm" ;
        Italian = ss "Italian" ;
        Expensive = ss "expensive" ;
        Delicious = ss "delicious" ;
        Boring = ss "boring" ;
    }

Partial application

The rule

    lin This k = prefix "this" k ;

can be written more concisely

    lin This = prefix "this" ;

Part of the art in functional programming: decide the order of arguments in a function, so that partial application can be used as much as possible.

For instance, prefix is typically applied to linearization variables with constant strings. Hence we put the Str argument before the SS argument.

Exercise. Define an operation infix analogous to prefix, such that it allows you to write

    lin Is = infix "is" ;

Testing resource modules

Import with the flag -retain,

    > import -retain StringOper.gf

Compute the value with compute_concrete = cc,

    > compute_concrete prefix "in" (ss "addition")
    {s : Str = "in" ++ "addition"}

Grammar architecture

Extending a grammar

A new module can extend an old one:

    abstract Morefood = Food ** {
      cat
        Question ;
      fun
        QIs : Item -> Quality -> Question ;
        Pizza : Kind ;
    }

Parallel to the abstract syntax, extensions can be built for concrete syntaxes:

    concrete MorefoodEng of Morefood = FoodEng ** {
      lincat
        Question = {s : Str} ;
      lin
        QIs item quality = {s = "is" ++ item.s ++ quality.s} ;
        Pizza = {s = "pizza"} ;
    }

The effect of extension: all of the contents of the extended and extending modules are put together.

In other words: the new module inherits the contents of the old module.

Simultaneous extension and opening:

    concrete MorefoodIta of Morefood = FoodIta ** open StringOper in {
      lincat
        Question = SS ;
      lin
        QIs item quality = ss (item.s ++ "è" ++ quality.s) ;
        Pizza = ss "pizza" ;
    }

Resource modules can extend other resource modules - thus it is possible to build resource hierarchies.

Multiple inheritance

Extend several grammars at the same time:

    abstract Foodmarket = Food, Fruit, Mushroom ** {
      fun
        FruitKind    : Fruit    -> Kind ;
        MushroomKind : Mushroom -> Kind ;
      }

where

    abstract Fruit = {
      cat Fruit ;
      fun Apple, Peach : Fruit ;
    }
  
    abstract Mushroom = {
      cat Mushroom ;
      fun Cep, Agaric : Mushroom ;
    }

Exercise. Refactor Food by taking apart Wine into a special Drink module.

Lesson 3: Grammars with parameters

Goals:

It is possible to skip this chapter and go directly to the next, since the use of the GF Resource Grammar library makes it unnecessary to use parameters: they could be left to library implementors.

The problem: words have to be inflected

Plural forms are needed in things like

these Italian wines are delicious

This requires two things:

Different languages have different types of inflection and agreement.

In a multilingual grammar, we want to ignore such distinctions in abstract syntax.

Exercise. Make a list of the possible forms that nouns, adjectives, and verbs can have in some languages that you know.

Parameters and tables

We define the parameter type of number in English by a new form of judgement:

    param Number = Sg | Pl ;

This judgement defines the parameter type Number by listing its two constructors, Sg and Pl (singular and plural).

We give Kind a linearization type that has a table depending on number:

    lincat Kind = {s : Number => Str} ;

The table type Number => Str is similar a function type (Number -> Str).

Difference: the argument must be a parameter type. Then the argument-value pairs can be listed in a finite table.

Here is a table:

    lin Cheese = {
      s = table {
        Sg => "cheese" ;
        Pl => "cheeses"
      }
    } ;

The table has branches, with a pattern on the left of the arrow => and a value on the right.

The application of a table is done by the selection operator !.

It which is computed by pattern matching: return the value from the first branch whose pattern matches the argument. For instance,

     table {Sg => "cheese" ; Pl => "cheeses"} ! Pl
     ===> "cheeses"

Case expressions are syntactic sugar:

    case e of {...} ===  table {...} ! e

Since they are familiar to Haskell and ML programmers, they can come out handy when writing GF programs.

Constructors can take arguments from other parameter types.

Example: forms of English verbs (except be):

    param VerbForm = VPresent Number | VPast | VPastPart | VPresPart ;

Fact expressed: only present tense has number variation.

Example table: the forms of the verb drink:

    table {
      VPresent Sg => "drinks" ;
      VPresent Pl => "drink" ;
      VPast       => "drank" ;
      VPastPart   => "drunk" ;
      VPresPart   => "drinking"
      }

Exercise. In an earlier exercise (previous section), you made a list of the possible forms that nouns, adjectives, and verbs can have in some languages that you know. Now take some of the results and implement them by using parameter type definitions and tables. Write them into a resource module, which you can test by using the command compute_concrete.

Inflection tables and paradigms

A morphological paradigm is a formula telling how a class of words is inflected.

From the GF point of view, a paradigm is a function that takes a lemma (also known as a dictionary form, or a citation form) and returns an inflection table.

The following operation defines the regular noun paradigm of English:

    oper regNoun : Str -> {s : Number => Str} = \dog -> {
      s = table {
        Sg => dog ;
        Pl => dog + "s"
        }
      } ;

The gluing operator + glues strings to one token:

    (regNoun "cheese").s ! Pl  ===> "cheese" + "s"  ===>  "cheeses"

A more complex example: regular verbs,

    oper regVerb : Str -> {s : VerbForm => Str} = \talk -> {
      s = table {
        VPresent Sg => talk + "s" ;
        VPresent Pl => talk ;
        VPresPart   => talk + "ing" ;
        _           => talk + "ed"
        }
      } ;

The catch-all case for the past tense and the past participle uses a wild card pattern _.

Exercises on morphology

  1. Identify cases in which the regNoun paradigm does not apply in English, and implement some alternative paradigms.

  2. Implement some regular paradigms for other languages you have considered in earlier exercises.

Using parameters in concrete syntax

Purpose: a more radical variation between languages than just the use of different words and word orders.

We add to the grammar Food two rules for forming plural items:

    fun These, Those : Kind -> Item ;

We also add a noun which in Italian has the feminine case:

    fun Pizza : Kind ;

This will force us to deal with gender-

Agreement

In English, the phrase-forming rule

    fun Is : Item -> Quality -> Phrase ;

is affected by the number because of subject-verb agreement: the verb of a sentence must be inflected in the number of the subject,

    Is (This Pizza) Warm   ===>  "this pizza is warm"
    Is (These Pizza) Warm  ===>  "these pizzas are warm"

It is the copula (the verb be) that is affected:

    oper copula : Number -> Str = \n ->
      case n of {
        Sg => "is" ;
        Pl => "are"
        } ;

The subject Item must have such a number to provide to the copula:

    lincat Item = {s : Str ; n : Number} ;

Now we can write

    lin Is item qual = {s = item.s ++ copula item.n ++ qual.s} ;

Determiners

How does an Item subject receive its number? The rules

    fun This, These : Kind -> Item ;

add determiners, either this or these, which require different this pizza vs. these pizzas.

Thus Kind must have both singular and plural forms:

    lincat Kind = {s : Number => Str} ;

We can write

    lin This kind = {
      s = "this" ++ kind.s ! Sg ;
      n = Sg
    } ;
  
    lin These kind = {
      s = "these" ++ kind.s ! Pl ;
      n = Pl
    } ;

To avoid copy-and-paste, we can factor out the pattern of determination,

    oper det :
      Str -> Number -> {s : Number => Str} -> {s : Str ; n : Number} =
        \det,n,kind -> {
        s = det ++ kind.s ! n ;
        n = n
      } ;

Now we can write

    lin This  = det Sg "this" ;
    lin These = det Pl "these" ;

In a more lexicalized grammar, determiners would be a category:

    lincat Det = {s : Str ; n : Number} ;
    fun Det : Det -> Kind -> Item ;
    lin Det det kind = {
        s = det.s ++ kind.s ! det.n ;
        n = det.n
      } ;

Parametric vs. inherent features

Kinds have number as a parametric feature: both singular and plural can be formed,

    lincat Kind = {s : Number => Str} ;

Items have number as an inherent feature: they are inherently either singular or plural,

    lincat Item = {s : Str ; n : Number} ;

Italian Kind will have parametric number and inherent gender:

    lincat Kind = {s : Number => Str ; g : Gender} ;

Questions to ask when designing parameters:

Dictionaries give good advice:

uomo, pl. uomini, n.m. "man"

tells that uomo is a masculine noun with the plural form uomini. Hence, parametric number and an inherent gender.

For words, inherent features are usually given as lexical information.

For combinations, they are inherited from some part of the construction (typically the one called the head). Italian modification:

    lin QKind qual kind =
      let gen = kind.g in {
        s = table {n => kind.s ! n ++ qual.s ! gen ! n} ;
        g = gen
        } ;

Notice

An English concrete syntax for Foods with parameters

We use some string operations from the library Prelude are used.

     concrete FoodsEng of Foods = open Prelude in {
  
    lincat
      S, Quality = SS ;
      Kind = {s : Number => Str} ;
      Item = {s : Str ; n : Number} ;
  
    lin
      Is item quality = ss (item.s ++ copula item.n ++ quality.s) ;
      This  = det Sg "this" ;
      That  = det Sg "that" ;
      These = det Pl "these" ;
      Those = det Pl "those" ;
      QKind quality kind = {s = table {n => quality.s ++ kind.s ! n}} ;
      Wine = regNoun "wine" ;
      Cheese = regNoun "cheese" ;
      Fish = noun "fish" "fish" ;
      Pizza = regNoun "pizza" ;
      Very = prefixSS "very" ;
      Fresh = ss "fresh" ;
      Warm = ss "warm" ;
      Italian = ss "Italian" ;
      Expensive = ss "expensive" ;
      Delicious = ss "delicious" ;
      Boring = ss "boring" ;

    param
      Number = Sg | Pl ;
  
    oper
      det : Number -> Str -> {s : Number => Str} -> {s : Str ; n : Number} =
        \n,d,cn -> {
          s = d ++ cn.s ! n ;
          n = n
        } ;
      noun : Str -> Str -> {s : Number => Str} =
        \man,men -> {s = table {
          Sg => man ;
          Pl => men
          }
        } ;
      regNoun : Str -> {s : Number => Str} =
        \car -> noun car (car + "s") ;
      copula : Number -> Str =
        \n -> case n of {
          Sg => "is" ;
          Pl => "are"
          } ;
    }

More on inflection paradigms

Let us extend the English noun paradigms so that we can deal with all nouns, not just the regular ones. The goal is to provide a morphology module that makes it easy to add words to a lexicon.

Worst-case functions

We perform data abstraction from the type of nouns by writing a a worst-case function:

    oper Noun : Type = {s : Number => Str} ;
  
    oper mkNoun : Str -> Str -> Noun = \x,y -> {
      s = table {
        Sg => x ;
        Pl => y
        }
      } ;
  
    oper regNoun : Str -> Noun = \x -> mkNoun x (x + "s") ;

Then we can define

    lincat N = Noun ;
    lin Mouse = mkNoun "mouse" "mice" ;
    lin House = regNoun "house" ;

where the underlying types are not seen.

We are free to change the undelying definitions, e.g. add case (nominative or genitive) to noun inflection:

    param Case = Nom | Gen ;
  
    oper Noun : Type = {s : Number => Case => Str} ;

Now we have to redefine the worst-case function

    oper mkNoun : Str -> Str -> Noun = \x,y -> {
      s = table {
        Sg => table {
          Nom => x ;
          Gen => x + "'s"
          } ;
        Pl => table {
          Nom => y ;
          Gen => y + case last y of {
            "s" => "'" ;
            _   => "'s"
          }
        }
      } ;

But up from this level, we can retain the old definitions

    lin Mouse = mkNoun "mouse" "mice" ;
    oper regNoun : Str -> Noun = \x -> mkNoun x (x + "s") ;

In the last definition of mkNoun, we used a case expression on the last character of the plural, as well as the Prelude operation

    last : Str -> Str ;

returning the string consisting of the last character.

The case expression uses pattern matching over strings, which is supported in GF, alongside with pattern matching over parameters.

Smart paradigms

The regular dog-dogs paradigm has predictable variations:

We could provide alternative paradigms:

    noun_y : Str -> Noun = \fly -> mkNoun fly (init fly + "ies") ;
    noun_s : Str -> Noun = \bus -> mkNoun bus (bus + "es") ;

(The Prelude function init drops the last character of a token.)

Drawbacks:

Better solution: a smart paradigm:

    regNoun : Str -> Noun = \w ->
      let
        ws : Str = case w of {
          _ + ("a" | "e" | "i" | "o") + "o" => w + "s" ;  -- bamboo
          _ + ("s" | "x" | "sh" | "o")      => w + "es" ; -- bus, hero
          _ + "z"                           => w + "zes" ;-- quiz
          _ + ("a" | "e" | "o" | "u") + "y" => w + "s" ;  -- boy
          x + "y"                           => x + "ies" ;-- fly
          _                                 => w + "s"    -- car
          }
      in
      mkNoun w ws

GF has regular expression patterns:

The patterns are ordered in such a way that, for instance, the suffix "oo" prevents bamboo from matching the suffix "o".

Exercises on regular patterns

  1. The same rules that form plural nouns in English also apply in the formation of third-person singular verbs. Write a regular verb paradigm that uses this idea, but first rewrite regNoun so that the analysis needed to build s-forms is factored out as a separate oper, which is shared with regVerb.

  2. Extend the verb paradigms to cover all verb forms in English, with special care taken of variations with the suffix ed (e.g. try-tried, use-used).

  3. Implement the German Umlaut operation on word stems. The operation changes the vowel of the stressed stem syllable as follows: a to ä, au to äu, o to ö, and u to ü. You can assume that the operation only takes syllables as arguments. Test the operation to see whether it correctly changes Arzt to Ärzt, Baum to Bäum, Topf to Töpf, and Kuh to Küh.

Function types with variables

In Lesson 5, dependent function types need a notation that binds a variable to the argument type, as in

    switchOff : (k : Kind) -> Action k

Function types without variables are actually a shorthand:

    PredVP : NP -> VP -> S

means

    PredVP : (x : NP) -> (y : VP) -> S

or any other naming of the variables.

Sometimes variables shorten the code, since they can share a type:

    octuple : (x,y,z,u,v,w,s,t : Str) -> Str

If a bound variable is not used, it can be replaced by a wildcard:

    octuple : (_,_,_,_,_,_,_,_ : Str) -> Str

A good practice is to indicate the number of arguments:

    octuple : (x1,_,_,_,_,_,_,x8 : Str) -> Str

For inflection paradigms, it is handy to use heuristic variable names, looking like the expected forms:

    mkNoun : (mouse,mice : Str) -> Noun

Separating operation types and definitions

In librarues, it is useful to group type signatures separately from definitions. It is possible to divide an oper judgement,

    oper regNoun : Str -> Noun ;
    oper regNoun s = mkNoun s (s + "s") ;

and put the parts in different places.

With the interface and instance module types (see here): the parts can even be put to different files.

Overloading of operations

Overloading: different functions can be given the same name, as e.g. in C++.

The compiler performs overload resolution, which works as long as the functions have different types.

In GF, the functions must be grouped together in overload groups.

Example: different ways to define nouns in English:

    oper mkN : overload {
      mkN : (dog : Str) -> Noun ;         -- regular nouns
      mkN : (mouse,mice : Str) -> Noun ;  -- irregular nouns
    }

Cf. dictionaries: if the word is regular, just one form is needed. If it is irregular, more forms are given.

The definition can be given separately, or at the same time, as the types:

    oper mkN = overload {
      mkN : (dog : Str) -> Noun = regNoun ;
      mkN : (mouse,mice : Str) -> Noun = mkNoun ;
    }

Exercise. Design a system of English verb paradigms presented by an overload group.

Morphological analysis and morphology quiz

The command morpho_analyse = ma can be used to read a text and return for each word its analyses (in the current grammar):

    > read_file bible.txt | morpho_analyse

The command morpho_quiz = mq generates inflection exercises.

    % gf alltenses/IrregFre.gfo
  
    > morpho_quiz -cat=V
  
    Welcome to GF Morphology Quiz.
    ...
  
    réapparaître : VFin VCondit  Pl  P2
    réapparaitriez
    > No, not réapparaitriez, but
    réapparaîtriez
    Score 0/1

The Italian Foods grammar

Parameters include not only number but also gender.

  concrete FoodsIta of Foods = open Prelude in {
  
    param
      Number = Sg | Pl ;
      Gender = Masc | Fem ;

Qualities are inflected for gender and number, whereas kinds have a parametric number and an inherent gender. Items have an inherent number and gender.

    lincat
      Phr = SS ;
      Quality = {s : Gender => Number => Str} ;
      Kind = {s : Number => Str ; g : Gender} ;
      Item = {s : Str ; g : Gender ; n : Number} ;

A Quality is an adjective, with one form for each gender-number combination.

    oper
      adjective : (_,_,_,_ : Str) -> {s : Gender => Number => Str} =
        \nero,nera,neri,nere -> {
          s = table {
            Masc => table {
              Sg => nero ;
              Pl => neri
              } ;
            Fem => table {
              Sg => nera ;
              Pl => nere
              }
            }
        } ;

Regular adjectives work by adding endings to the stem.

      regAdj : Str -> {s : Gender => Number => Str} = \nero ->
        let ner = init nero
        in adjective nero (ner + "a") (ner + "i") (ner + "e") ;

For noun inflection, we are happy to give the two forms and the gender explicitly:

      noun : Str -> Str -> Gender -> {s : Number => Str ; g : Gender} =
        \vino,vini,g -> {
          s = table {
            Sg => vino ;
            Pl => vini
            } ;
          g = g
        } ;

We need only number variation for the copula.

      copula : Number -> Str =
        \n -> case n of {
          Sg => "è" ;
          Pl => "sono"
          } ;

Determination is more complex than in English, because of gender:

      det : Number -> Str -> Str -> {s : Number => Str ; g : Gender} ->
          {s : Str ; g : Gender ; n : Number} =
        \n,m,f,cn -> {
          s = case cn.g of {Masc => m ; Fem => f} ++ cn.s ! n ;
          g = cn.g ;
          n = n
        } ;

The complete set of linearization rules:

    lin
      Is item quality =
        ss (item.s ++ copula item.n ++ quality.s ! item.g ! item.n) ;
      This  = det Sg "questo" "questa" ;
      That  = det Sg "quel"   "quella" ;
      These = det Pl "questi" "queste" ;
      Those = det Pl "quei"   "quelle" ;
      QKind quality kind = {
        s = \\n => kind.s ! n ++ quality.s ! kind.g ! n ;
        g = kind.g
        } ;
      Wine = noun "vino" "vini" Masc ;
      Cheese = noun "formaggio" "formaggi" Masc ;
      Fish = noun "pesce" "pesci" Masc ;
      Pizza = noun "pizza" "pizze" Fem ;
      Very qual = {s = \\g,n => "molto" ++ qual.s ! g ! n} ;
      Fresh = adjective "fresco" "fresca" "freschi" "fresche" ;
      Warm = regAdj "caldo" ;
      Italian = regAdj "italiano" ;
      Expensive = regAdj "caro" ;
      Delicious = regAdj "delizioso" ;
      Boring = regAdj "noioso" ;
    }

Exercises on using parameters

  1. Experiment with multilingual generation and translation in the Foods grammars.

  2. Add items, qualities, and determiners to the grammar, and try to get their inflection and inherent features right.

  3. Write a concrete syntax of Food for a language of your choice, now aiming for complete grammatical correctness by the use of parameters.

  4. Measure the size of the context-free grammar corresponding to FoodsIta. You can do this by printing the grammar in the context-free format (print_grammar -printer=bnf) and counting the lines.

Discontinuous constituents

A linearization record may contain more strings than one, and those strings can be put apart in linearization.

Example: English particle verbs, (switch off). The object can appear between:

he switched it off

The verb switch off is called a discontinuous constituents.

We can define transitive verbs and their combinations as follows:

    lincat V2 = {s : Number => Str ; part : Str} ;
  
    fun AppV2 : Item -> V2 -> Item -> Phrase ;
  
    lin AppV2 subj v2 obj =
      {s = subj.s ++ v2.s ! subj.n ++ obj.s ++ v2.part} ;

Exercise. Define the language a^n b^n c^n in GF, i.e. any number of a's followed by the same number of b's and the same number of c's. This language is not context-free, but can be defined in GF by using discontinuous constituents.

Strings at compile time vs. run time

Tokens are created in the following ways:

Since tokens must be known at compile time, the above operations may not be applied to run-time variables (i.e. variables that stand for function arguments in linearization rules).

Hence it is not legal to write

    cat Noun ;
    fun Plural : Noun -> Noun ;
    lin Plural n = {s = n.s + "s"} ;

because n is a run-time variable. Also

    lin Plural n = {s = (regNoun n).s ! Pl} ;

is incorrect with regNoun as defined here, because the run-time variable is eventually sent to string pattern matching and gluing.

How to write tokens together without a space?

    lin Question p = {s = p + "?"} ;

is incorrect.

The way to go is to use an unlexer that creates correct spacing after linearization.

Correspondingly, a lexer that e.g. analyses "warm?" into to tokens is needed before parsing. This topic will be covered in here.

Supplementary constructs for concrete syntax

Record extension and subtyping

The symbol ** is used for both record types and record objects.

    lincat V2 = Verb ** {c : Case} ;
  
    lin Follow = regVerb "folgen" ** {c = Dative} ;

V2 (transitive verb) becomes a subtype of Verb.

If T is a subtype of R, an object of T can be used whenever an object of R is required.

Covariance: a function returning a record T as value can also be used to return a value of a supertype R.

Contravariance: a function taking an R as argument can also be applied to any object of a subtype T.

Tuples and product types

Product types and tuples are syntactic sugar for record types and records:

    T1 * ... * Tn   ===   {p1 : T1 ; ... ; pn : Tn}
    <t1, ...,  tn>  ===   {p1 = T1 ; ... ; pn = Tn}

Thus the labels p1, p2,... are hard-coded.

Prefix-dependent choices

English indefinite article:

    oper artIndef : Str =
       pre {
         ("a" | "e" | "i" | "o") => "an" ;
         _ => "a"
       } ;

Thus

    artIndef ++ "cheese"  --->  "a" ++ "cheese"
    artIndef ++ "apple"   --->  "an" ++ "apple"

Lesson 4: Using the resource grammar library

Goals:

The coverage of the library

The current 16 resource languages (GF version 3.2, December 2010) are

The first three letters (Eng etc) are used in grammar module names (ISO 639-3 standard).

The structure of the library

Semantic grammars (up to now in this tutorial): a grammar defines a system of meanings (abstract syntax) and tells how they are expressed(concrete syntax).

Resource grammars (as usual in linguistic tradition): a grammar specifies the grammatically correct combinations of words, whatever their meanings are.

With resource grammars, we can achieve a wider coverage than with semantic grammars.

Lexical vs. phrasal rules

A resource grammar has two kinds of categories and two kinds of rules:

GE makes no formal distinction between these two kinds.

But it is a good discipline to follow.

Lexical categories

Two kinds of lexical categories:

Lexical rules

Closed classes: module Syntax. In the Foods grammar, we need

    this_Det, that_Det, these_Det, those_Det : Det ;
    very_AdA  : AdA ;

Naming convention: word followed by the category (so we can distinguish the quantifier that from the conjunction that).

Open classes have no objects in Syntax. Words are built as they are needed in applications: if we have

    fun Wine : Kind ;

we will define

    lin Wine = mkN "wine" ;

where we use mkN from ParadigmsEng:

Resource lexicon

Alternative concrete syntax for

    fun Wine : Kind ;

is to provide a resource lexicon, which contains definitions such as

    oper wine_N : N = mkN "wine" ;

so that we can write

    lin Wine = wine_N ;

Advantages:

Phrasal categories

In Foods, we need just four phrasal categories:

    Cl ;   -- clause             e.g. "this pizza is good"
    NP ;   -- noun phrase        e.g. "this pizza"
    CN ;   -- common noun        e.g. "warm pizza"
    AP ;   -- adjectival phrase  e.g. "very warm"

Clauses are similar to sentences (S), but without a fixed tense and mood; see here for how they relate.

Common nouns are made into noun phrases by adding determiners.

Syntactic combinations

We need the following combinations:

    mkCl : NP -> AP -> Cl ;      -- e.g. "this pizza is very warm"
    mkNP : Det -> CN -> NP ;     -- e.g. "this pizza"
    mkCN : AP -> CN -> CN ;      -- e.g. "warm pizza"
    mkAP : AdA -> AP -> AP ;     -- e.g. "very warm"

We also need lexical insertion, to form phrases from single words:

    mkCN : N -> CN ;
    mkAP : A -> AP ;

Naming convention: to construct a C, use a function mkC.

Heavy overloading: the current library (version 1.2) has 23 operations named mkNP!

Example syntactic combination

The sentence

these very warm pizzas are Italian

can be built as follows:

    mkCl
      (mkNP these_Det
         (mkCN (mkAP very_AdA (mkAP warm_A)) (mkCN pizza_N)))
      (mkAP italian_AP)

The task now: to define the concrete syntax of Foods so that this syntactic tree gives the value of linearizing the semantic tree

    Is (These (QKind (Very Warm) Pizza)) Italian

The resource API

Language-specific and language-independent parts - roughly,

Full API documentation on-line: the resource synopsis,

grammaticalframework.org/lib/doc/synopsis.html

A miniature resource API: categories

Category

Explanation

Example

Cl

clause (sentence), with all tenses

she looks at this

AP

adjectival phrase

very warm

CN

common noun (without determiner)

red house

NP

noun phrase (subject or object)

the red house

AdA

adjective-modifying adverb,

very

Det

determiner

these

A

one-place adjective

warm

N

common noun

house

A miniature resource API: rules

Function

Type

Example

mkCl

NP -> AP -> Cl

John is very old

mkNP

Det -> CN -> NP

these old man

mkCN

N -> CN

house

mkCN

AP -> CN -> CN

very big blue house

mkAP

A -> AP

old

mkAP

AdA -> AP -> AP

very very old

A miniature resource API: structural words

Function

Type

In English

this_Det

Det

this

that_Det

Det

that

these_Det

Det

this

those_Det

Det

that

very_AdA

AdA

very

A miniature resource API: paradigms

From ParadigmsEng:

Function

Type

mkN

(dog : Str) -> N

mkN

(man,men : Str) -> N

mkA

(cold : Str) -> A

From ParadigmsIta:

Function

Type

mkN

(vino : Str) -> N

mkA

(caro : Str) -> A

A miniature resource API: more paradigms

From ParadigmsGer:

Function

Type

Gender

Type

masculine

Gender

feminine

Gender

neuter

Gender

mkN

(Stufe : Str) -> N

mkN

(Bild,Bilder : Str) -> Gender -> N

mkA

(klein : Str) -> A

mkA

(gut,besser,beste : Str) -> A

From ParadigmsFin:

Function

Type

mkN

(talo : Str) -> N

mkA

(hieno : Str) -> A

Exercises

1. Try out the morphological paradigms in different languages. Do as follows:

    > i -path=alltenses -retain alltenses/ParadigmsGer.gfo
    > cc -table mkN "Farbe"
    > cc -table mkA "gut" "besser" "beste"

Example: English

We assume the abstract syntax Foods from Lesson 3.

We don't need to think about inflection and agreement, but just pick functions from the resource grammar library.

We need a path with

Thus the beginning of the module is

    --# -path=.:../foods:present
  
    concrete FoodsEng of Foods = open SyntaxEng,ParadigmsEng in {

English example: linearization types and combination rules

As linearization types, we use clauses for Phrase, noun phrases for Item, common nouns for Kind, and adjectival phrases for Quality.

    lincat
      Phrase = Cl ;
      Item = NP ;
      Kind = CN ;
      Quality = AP ;

Now the combination rules we need almost write themselves automatically:

    lin
      Is item quality = mkCl item quality ;
      This kind = mkNP this_Det kind ;
      That kind = mkNP that_Det kind ;
      These kind = mkNP these_Det kind ;
      Those kind = mkNP those_Det kind ;
      QKind quality kind = mkCN quality kind ;
      Very quality = mkAP very_AdA quality ;

English example: lexical rules

We use resource paradigms and lexical insertion rules.

The two-place noun paradigm is needed only once, for fish - everythins else is regular.

      Wine = mkCN (mkN "wine") ;
      Pizza = mkCN (mkN "pizza") ;
      Cheese = mkCN (mkN "cheese") ;
      Fish = mkCN (mkN "fish" "fish") ;
      Fresh = mkAP (mkA "fresh") ;
      Warm = mkAP (mkA "warm") ;
      Italian = mkAP (mkA "Italian") ;
      Expensive = mkAP (mkA "expensive") ;
      Delicious = mkAP (mkA "delicious") ;
      Boring = mkAP (mkA "boring") ;
    }

English example: exercises

1. Compile the grammar FoodsEng and generate and parse some sentences.

2. Write a concrete syntax of Foods for Italian or some other language included in the resource library. You can compare the results with the hand-written grammars presented earlier in this tutorial.

Functor implementation of multilingual grammars

New language by copy and paste

If you write a concrete syntax of Foods for some other language, much of the code will look exactly the same as for English. This is because

But lexical rules are more language-dependent.

Thus, to port a grammar to a new language, you

  1. copy the concrete syntax of a given language
  2. change the words (strings and inflection paradigms)

Can we avoid this programming by copy-and-paste?

Functors: functions on the module level

Functors familiar from the functional programming languages ML and OCaml, also known as parametrized modules.

In GF, a functor is a module that opens one or more interfaces.

An interface is a module similar to a resource, but it only contains the types of opers, not (necessarily) their definitions.

Syntax for functors: add the keyword incomplete. We will use the header

    incomplete concrete FoodsI of Foods = open Syntax, LexFoods in

where

    interface Syntax    -- the resource grammar interface
    interface LexFoods  -- the domain lexicon interface

When we moreover have

    instance SyntaxEng of Syntax     -- the English resource grammar
    instance LexFoodsEng of LexFoods -- the English domain lexicon

we can write a functor instantiation,

    concrete FoodsGer of Foods = FoodsI with
      (Syntax = SyntaxGer),
      (LexFoods = LexFoodsGer) ;

Code for the Foods functor

    --# -path=.:../foods
  
    incomplete concrete FoodsI of Foods = open Syntax, LexFoods in {
    lincat
      Phrase = Cl ;
      Item = NP ;
      Kind = CN ;
      Quality = AP ;
    lin
      Is item quality = mkCl item quality ;
      This kind = mkNP this_Det kind ;
      That kind = mkNP that_Det kind ;
      These kind = mkNP these_Det kind ;
      Those kind = mkNP those_Det kind ;
      QKind quality kind = mkCN quality kind ;
      Very quality = mkAP very_AdA quality ;
  
      Wine = mkCN wine_N ;
      Pizza = mkCN pizza_N ;
      Cheese = mkCN cheese_N ;
      Fish = mkCN fish_N ;
      Fresh = mkAP fresh_A ;
      Warm = mkAP warm_A ;
      Italian = mkAP italian_A ;
      Expensive = mkAP expensive_A ;
      Delicious = mkAP delicious_A ;
      Boring = mkAP boring_A ;
    }

Code for the LexFoods interface

    interface LexFoods = open Syntax in {
    oper
      wine_N : N ;
      pizza_N : N ;
      cheese_N : N ;
      fish_N : N ;
      fresh_A : A ;
      warm_A : A ;
      italian_A : A ;
      expensive_A : A ;
      delicious_A : A ;
      boring_A : A ;
    }

Code for a German instance of the lexicon

    instance LexFoodsGer of LexFoods = open SyntaxGer, ParadigmsGer in {
    oper
      wine_N = mkN "Wein" ;
      pizza_N = mkN "Pizza" "Pizzen" feminine ;
      cheese_N = mkN "Käse" "Käsen" masculine ;
      fish_N = mkN "Fisch" ;
      fresh_A = mkA "frisch" ;
      warm_A = mkA "warm" "wärmer" "wärmste" ;
      italian_A = mkA "italienisch" ;
      expensive_A = mkA "teuer" ;
      delicious_A = mkA "köstlich" ;
      boring_A = mkA "langweilig" ;
    }

Code for a German functor instantiation

    --# -path=.:../foods:present
  
    concrete FoodsGer of Foods = FoodsI with
      (Syntax = SyntaxGer),
      (LexFoods = LexFoodsGer) ;

Adding languages to a functor implementation

Just two modules are needed:

The functor instantiation is completely mechanical to write.

The domain lexicon instance requires some knowledge of the words of the language:

Example: adding Finnish

Lexicon instance

    instance LexFoodsFin of LexFoods = open SyntaxFin, ParadigmsFin in {
    oper
      wine_N = mkN "viini" ;
      pizza_N = mkN "pizza" ;
      cheese_N = mkN "juusto" ;
      fish_N = mkN "kala" ;
      fresh_A = mkA "tuore" ;
      warm_A = mkA "lämmin" ;
      italian_A = mkA "italialainen" ;
      expensive_A = mkA "kallis" ;
      delicious_A = mkA "herkullinen" ;
      boring_A = mkA "tylsä" ;
    }

Functor instantiation

    --# -path=.:../foods:present
  
    concrete FoodsFin of Foods = FoodsI with
      (Syntax = SyntaxFin),
      (LexFoods = LexFoodsFin) ;

A design pattern

This can be seen as a design pattern for multilingual grammars:

                        concrete DomainL*
  
      instance LexDomainL                 instance SyntaxL*
  
                   incomplete concrete DomainI
                   /           |              \
     interface LexDomain   abstract Domain    interface Syntax*

Modules marked with * are either given in the library, or trivial.

Of the hand-written modules, only LexDomainL is language-dependent.

Functors: exercises

1. Compile and test FoodsGer.

2. Refactor FoodsEng into a functor instantiation.

3. Instantiate the functor FoodsI to some language of your choice.

4. Design a small grammar that can be used for controlling an MP3 player. The grammar should be able to recognize commands such as play this song, with the following variations:

The implementation goes in the following phases:

  1. abstract syntax
  2. (optional:) prototype string-based concrete syntax
  3. functor over resource syntax and lexicon interface
  4. lexicon instance for the first language
  5. functor instantiation for the first language
  6. lexicon instance for the second language
  7. functor instantiation for the second language
  8. ...

Restricted inheritance

A problem with functors

Problem: a functor only works when all languages use the resource Syntax in the same way.

Example (contrived): assume that English has no word for Pizza, but has to use the paraphrase Italian pie. This is no longer a noun N, but a complex phrase in the category CN.

Possible solution: change interface the LexFoods with

    oper pizza_CN : CN ;

Problem with this solution:

Restricted inheritance: include or exclude

A module may inherit just a selection of names.

Example: the FoodMarket example "Rsecarchitecture:

    abstract Foodmarket = Food, Fruit [Peach], Mushroom - [Agaric]

Here, from Fruit we include Peach only, and from Mushroom we exclude Agaric.

A concrete syntax of Foodmarket must make the analogous restrictions.

The functor problem solved

The English instantiation inherits the functor implementation except for the constant Pizza. This constant is defined in the body instead:

    --# -path=.:../foods:present
  
    concrete FoodsEng of Foods = FoodsI - [Pizza] with
      (Syntax = SyntaxEng),
      (LexFoods = LexFoodsEng) **
        open SyntaxEng, ParadigmsEng in {
  
      lin Pizza = mkCN (mkA "Italian") (mkN "pie") ;
    }

Grammar reuse

Abstract syntax modules can be used as interfaces, and concrete syntaxes as their instances.

The following correspondencies are then applied:

    cat C         <--->  oper C : Type
  
    fun f : A     <--->  oper f : A
  
    lincat C = T  <--->  oper C : Type = T
  
    lin f = t     <--->  oper f : A = t

Library exercises

1. Find resource grammar terms for the following English phrases (in the category Phr). You can first try to build the terms manually.

every man loves a woman

this grammar speaks more than ten languages

which languages aren't in the grammar

which languages did you want to speak

Then translate the phrases to other languages.

Tenses

In Foods grammars, we have used the path

    --# -path=.:../foods

The library subdirectory present is a restricted version of the resource, with only present tense of verbs and sentences.

By just changing the path, we get all tenses:

    --# -path=.:../foods:alltenses

Now we can see all the tenses of phrases, by using the -all flag in linearization:

    > gr | l -all
    This wine is delicious
    Is this wine delicious
    This wine isn't delicious
    Isn't this wine delicious
    This wine is not delicious
    Is this wine not delicious
    This wine has been delicious
    Has this wine been delicious
    This wine hasn't been delicious
    Hasn't this wine been delicious
    This wine has not been delicious
    Has this wine not been delicious
    This wine was delicious
    Was this wine delicious
    This wine wasn't delicious
    Wasn't this wine delicious
    This wine was not delicious
    Was this wine not delicious
    This wine had been delicious
    Had this wine been delicious
    This wine hadn't been delicious
    Hadn't this wine been delicious
    This wine had not been delicious
    Had this wine not been delicious
    This wine will be delicious
    Will this wine be delicious
    This wine won't be delicious
    Won't this wine be delicious
    This wine will not be delicious
    Will this wine not be delicious
    This wine will have been delicious
    Will this wine have been delicious
    This wine won't have been delicious
    Won't this wine have been delicious
    This wine will not have been delicious
    Will this wine not have been delicious
    This wine would be delicious
    Would this wine be delicious
    This wine wouldn't be delicious
    Wouldn't this wine be delicious
    This wine would not be delicious
    Would this wine not be delicious
    This wine would have been delicious
    Would this wine have been delicious
    This wine wouldn't have been delicious
    Wouldn't this wine have been delicious
    This wine would not have been delicious
    Would this wine not have been delicious

We also see

The list is even longer in languages that have more tenses and moods, e.g. the Romance languages.

Lesson 5: Refining semantics in abstract syntax

Goals:

Dependent types

Problem: to express conditions of semantic well-formedness.

Example: a voice command system for a "smart house" wants to eliminate meaningless commands.

Thus we want to restrict particular actions to particular devices - we can dim a light, but we cannot dim a fan.

The following example is borrowed from the Regulus Book (Rayner & al. 2006).

A simple example is a "smart house" system, which defines voice commands for household appliances.

A dependent type system

Ontology:

Abstract syntax formalizing this:

    cat
      Command ;
      Kind ;
      Device Kind ; -- argument type Kind
      Action Kind ;
    fun
      CAction : (k : Kind) -> Action k -> Device k -> Command ;

Device and Action are both dependent types.

Examples of devices and actions

Assume the kinds light and fan,

    light, fan : Kind ;
    dim : Action light ;

Given a kind, k, you can form the device the k.

    DKindOne  : (k : Kind) -> Device k ;  -- the light

Now we can form the syntax tree

    CAction light dim (DKindOne light)

but we cannot form the trees

    CAction light dim (DKindOne fan)
    CAction fan   dim (DKindOne light)
    CAction fan   dim (DKindOne fan)

Linearization and parsing with dependent types

Concrete syntax does not know if a category is a dependent type.

    lincat Action = {s : Str} ;
    lin CAction _ act dev = {s = act.s ++ dev.s} ;

Notice that the Kind argument is suppressed in linearization.

Parsing with dependent types consists of two phases:

  1. context-free parsing

  2. filtering through type checker

    Parsing a type-correct command works as expected:

        > parse "dim the light"
    CAction light dim (DKindOne light)

    However, type-incorrect commands are rejected by the typecheck:

        > parse "dim the fan"
    The parsing is successful but the type checking failed with error(s):
      Couldn't match expected type Device light
         against the interred type Device fan
      In the expression: DKindOne fan

    ==Polymorphism==

    Sometimes an action can be performed on all kinds of devices.

    This is represented as a function that takes a Kind as an argument and produce an Action for that Kind:

        fun switchOn, switchOff : (k : Kind) -> Action k ;

    Functions of this kind are called polymorphic.

    We can use this kind of polymorphism in concrete syntax as well, to express Haskell-type library functions:

        oper const :(a,b : Type) -> a -> b -> a =
      \_,_,c,_ -> c ;
  
    oper flip : (a,b,c : Type) -> (a -> b ->c) -> b -> a -> c =
      \_,_,_,f,x,y -> f y x ;

    ===Dependent types: exercises===

    1. Write an abstract syntax module with above contents and an appropriate English concrete syntax. Try to parse the commands dim the light and dim the fan.

    2. Perform random and exhaustive generation.

    3. Add some device kinds and actions to the grammar.

Proof objects

Curry-Howard isomorphism = propositions as types principle: a proposition is a type of proofs (= proof objects).

Example: define the less than proposition for natural numbers,

    cat Nat ;
    fun Zero : Nat ;
    fun Succ : Nat -> Nat ;

Define inductively what it means for a number x to be less than a number y:

Expressing these axioms in type theory with a dependent type Less x y and two functions constructing its objects:

    cat Less Nat Nat ;
    fun lessZ : (y : Nat) -> Less Zero (Succ y) ;
    fun lessS : (x,y : Nat) -> Less x y -> Less (Succ x) (Succ y) ;

Example: the fact that 2 is less that 4 has the proof object

    lessS (Succ Zero) (Succ (Succ (Succ Zero)))
          (lessS Zero (Succ (Succ Zero)) (lessZ (Succ Zero)))
     : Less (Succ (Succ Zero)) (Succ (Succ (Succ (Succ Zero))))

Proof-carrying documents

Idea: to be semantically well-formed, the abstract syntax of a document must contain a proof of some property, although the proof is not shown in the concrete document.

Example: documents describing flight connections:

To fly from Gothenburg to Prague, first take LH3043 to Frankfurt, then OK0537 to Prague.

The well-formedness of this text is partly expressible by dependent typing:

    cat
      City ;
      Flight City City ;
    fun
      Gothenburg, Frankfurt, Prague : City ;
      LH3043 : Flight Gothenburg Frankfurt ;
      OK0537 : Flight Frankfurt Prague ;

To extend the conditions to flight connections, we introduce a category of proofs that a change is possible:

    cat IsPossible (x,y,z : City)(Flight x y)(Flight y z) ;

A legal connection is formed by the function

    fun Connect : (x,y,z : City) ->
      (u : Flight x y) -> (v : Flight y z) ->
        IsPossible x y z u v -> Flight x z ;

Restricted polymorphism

Above, all Actions were either of

To make this scale up for new Kinds, we can refine this to restricted polymorphism: defined for Kinds of a certain class

The notion of class uses the Curry-Howard isomorphism as follows:

Example: classes for switching and dimming

We modify the smart house grammar:

  cat
    Switchable Kind ;
    Dimmable   Kind ;
  fun
    switchable_light : Switchable light ;
    switchable_fan   : Switchable fan ;
    dimmable_light   : Dimmable light ;
  
    switchOn : (k : Kind) -> Switchable k -> Action k ;
    dim      : (k : Kind) -> Dimmable k -> Action k ;

Classes for new actions can be added incrementally.

Variable bindings

Mathematical notation and programming languages have expressions that bind variables.

Example: universal quantifier formula

    (All x)B(x)

The variable x has a binding (All x), and occurs bound in the body B(x).

Examples from informal mathematical language:

    for all x, x is equal to x
  
    the function that for any numbers x and y returns the maximum of x+y
    and x*y
  
    Let x be a natural number. Assume that x is even. Then x + 3 is odd.

Higher-order abstract syntax

Abstract syntax can use functions as arguments:

    cat Ind ; Prop ;
    fun All : (Ind -> Prop) -> Prop

where Ind is the type of individuals and Prop, the type of propositions.

Let us add an equality predicate

    fun Eq : Ind -> Ind -> Prop

Now we can form the tree

    All (\x -> Eq x x)

which we want to relate to the ordinary notation

    (All x)(x = x)

In higher-order abstract syntax (HOAS), all variable bindings are expressed using higher-order syntactic constructors.

Higher-order abstract syntax: linearization

HOAS has proved to be useful in the semantics and computer implementation of variable-binding expressions.

How do we relate HOAS to the concrete syntax?

In GF, we write

    fun All : (Ind -> Prop) -> Prop
    lin All B = {s = "(" ++ "All" ++ B.$0 ++ ")" ++ B.s}

General rule: if an argument type of a fun function is a function type A -> C, the linearization type of this argument is the linearization type of C together with a new field $0 : Str.

The argument B thus has the linearization type

    {s : Str ; $0 : Str},

If there are more bindings, we add $1, $2, etc.

Eta expansion

To make sense of linearization, syntax trees must be eta-expanded: for any function of type

    A -> B

an eta-expanded syntax tree has the form

    \x -> b

where b : B under the assumption x : A.

Given the linearization rule

    lin Eq a b = {s = "(" ++ a.s ++ "=" ++ b.s ++ ")"}

the linearization of the tree

    \x -> Eq x x

is the record

    {$0 = "x", s = ["( x = x )"]}

Then we can compute the linearization of the formula,

    All (\x -> Eq x x)  --> {s = "[( All x ) ( x = x )]"}.

The linearization of the variable x is, "automagically", the string "x".

Parsing variable bindings

GF can treat any one-word string as a variable symbol.

    > p -cat=Prop "( All x ) ( x = x )"
    All (\x -> Eq x x)

Variables must be bound if they are used:

    > p -cat=Prop "( All x ) ( x = y )"
    no tree found

Exercises on variable bindings

1. Write an abstract syntax of the whole predicate calculus, with the connectives "and", "or", "implies", and "not", and the quantifiers "exists" and "for all". Use higher-order functions to guarantee that unbounded variables do not occur.

2. Write a concrete syntax for your favourite notation of predicate calculus. Use Latex as target language if you want nice output. You can also try producing boolean expressions of some programming language. Use as many parenthesis as you need to guarantee non-ambiguity.

Semantic definitions

The fun judgements of GF are declarations of functions, giving their types.

Can we compute fun functions?

Mostly we are not interested, since functions are seen as constructors, i.e. data forms - as usual with

    fun Zero : Nat ;
    fun Succ : Nat -> Nat ;

But it is also possible to give semantic definitions to functions. The key word is def:

    fun one : Nat ;
    def one = Succ Zero ;
  
    fun twice : Nat -> Nat ;
    def twice x = plus x x ;
  
    fun plus : Nat -> Nat -> Nat ;
    def
      plus x Zero = x ;
      plus x (Succ y) = Succ (Sum x y) ;

Computing a tree

Computation: follow a chain of definition until no definition can be applied,

    plus one one -->
    plus (Succ Zero) (Succ Zero) -->
    Succ (plus (Succ Zero) Zero) -->
    Succ (Succ Zero)

Computation in GF is performed with the put_term command and the compute transformation, e.g.

    > parse -tr "1 + 1" | put_term -transform=compute -tr | l
    plus one one
    Succ (Succ Zero)
    s(s(0))

Definitional equality

Two trees are definitionally equal if they compute into the same tree.

Definitional equality does not guarantee sameness of linearization:

    plus one one     ===> 1 + 1
    Succ (Succ Zero) ===> s(s(0))

The main use of this concept is in type checking: sameness of types.

Thus e.g. the following types are equal

    Less Zero one
    Less Zero (Succ Zero))

so that an object of one also is an object of the other.

Judgement forms for constructors

The judgement form data tells that a category has certain functions as constructors:

    data Nat = Succ | Zero ;

The type signatures of constructors are given separately,

    fun Zero : Nat ;
    fun Succ : Nat -> Nat ;

There is also a shorthand:

    data Succ : Nat -> Nat ;    ===   fun Succ : Nat -> Nat ;
                                      data Nat = Succ ;

Notice: in def definitions, identifier patterns not marked as data will be treated as variables.

Exercises on semantic definitions

1. Implement an interpreter of a small functional programming language with natural numbers, lists, pairs, lambdas, etc. Use higher-order abstract syntax with semantic definitions. As concrete syntax, use your favourite programming language.

2. There is no termination checking for def definitions. Construct an examples that makes type checking loop. Type checking can be invoked with put_term -transform=solve.

Lesson 6: Grammars of formal languages

Goals:

Arithmetic expressions

We construct a calculator with addition, subtraction, multiplication, and division of integers.

    abstract Calculator = {
    flags startcat = Exp ;
    
    cat Exp ;
  
    fun
      EPlus, EMinus, ETimes, EDiv : Exp -> Exp -> Exp ;
      EInt : Int -> Exp ;
    }

The category Int is a built-in category of integers. Its syntax trees integer literals, i.e. sequences of digits:

    5457455814608954681 : Int

These are the only objects of type Int: grammars are not allowed to declare functions with Int as value type.

Concrete syntax: a simple approach

We begin with a concrete syntax that always uses parentheses around binary operator applications:

    concrete CalculatorP of Calculator = open Prelude in {
  
    lincat
      Exp = SS ;
    lin
      EPlus  = infix "+" ;
      EMinus = infix "-" ;
      ETimes = infix "*" ;
      EDiv   = infix "/" ;
      EInt i = i ;
  
    oper
      infix : Str -> SS -> SS -> SS = \f,x,y ->
        ss ("(" ++ x.s ++ f ++ y.s ++ ")") ;
    }

Now we have

    > linearize EPlus (EInt 2) (ETimes (EInt 3) (EInt 4))
    ( 2 + ( 3 * 4 ) )

First problems:

Lexing and unlexing

The input of parsing in GF is not just a string, but a list of tokens, returned by a lexer.

The default lexer in GF returns chunks separated by spaces:

    "(12 + (3 * 4))"  ===>  "(12", "+", "(3". "*". "4))"

The proper way would be

    "(", "12", "+", "(", "3", "*", "4", ")", ")"

Moreover, the tokens "12", "3", and "4" should be recognized as integer literals - they cannot be found in the grammar.

Lexers are invoked by flags to the command put_string = ps.

    > put_string -lexcode "(2 + (3 * 4))"
    ( 2 + ( 3 * 4 ) )

This can be piped into a parser, as usual:

    > ps -lexcode "(2 + (3 * 4))" | parse
    EPlus (EInt 2) (ETimes (EInt 3) (EInt 4))

In linearization, we use a corresponding unlexer:

    > linearize EPlus (EInt 2) (ETimes (EInt 3) (EInt 4)) | ps -unlexcode
    (2 + (3 * 4))

Most common lexers and unlexers

lexer

unlexer

description

chars

unchars

each character is a token

lexcode

unlexcode

program code conventions (uses Haskell's lex)

lexmixed

unlexmixed

like text, but between $ signs like code

lextext

unlextext

with conventions on punctuation and capitals

words

unwords

(default) tokens separated by space characters

Precedence and fixity

Arithmetic expressions should be unambiguous. If we write

    2 + 3 * 4

it should be parsed as one, but not both, of

    EPlus (EInt 2) (ETimes (EInt 3) (EInt 4))
    ETimes (EPlus (EInt 2) (EInt 3)) (EInt 4)

We choose the former tree, because multiplication has higher precedence than addition.

To express the latter tree, we have to use parentheses:

    (2 + 3) * 4

The usual precedence rules:

Precedence as a parameter

Precedence can be made into an inherent feature of expressions:

    oper
      Prec : PType = Ints 2 ;
      TermPrec : Type = {s : Str ; p : Prec} ;
  
      mkPrec : Prec -> Str -> TermPrec = \p,s -> {s = s ; p = p} ;
  
    lincat
      Exp = TermPrec ;

Notice Ints 2: a parameter type, whose values are the integers 0,1,2.

Using precedence levels: compare the inherent precedence of an expression with the expected precedence.

This idea is encoded in the operation

    oper usePrec : TermPrec -> Prec -> Str = \x,p ->
      case lessPrec x.p p of {
        True  => "(" x.s ")" ;
        False => x.s
      } ;

(We use lessPrec from lib/prelude/Formal.)

Fixities

We can define left-associative infix expressions:

    infixl : Prec -> Str -> (_,_ : TermPrec) -> TermPrec = \p,f,x,y ->
      mkPrec p (usePrec x p ++ f ++ usePrec y (nextPrec p)) ;

Constant-like expressions (the highest level):

    constant : Str -> TermPrec = mkPrec 2 ;

All these operations can be found in lib/prelude/Formal, which has 5 levels.

Now we can write the whole concrete syntax of Calculator compactly:

    concrete CalculatorC of Calculator = open Formal, Prelude in {
  
    flags lexer = codelit ; unlexer = code ; startcat = Exp ;
  
    lincat Exp = TermPrec ;
  
    lin
      EPlus  = infixl 0 "+" ;
      EMinus = infixl 0 "-" ;
      ETimes = infixl 1 "*" ;
      EDiv   = infixl 1 "/" ;
      EInt i = constant i.s ;
    }

Exercises on precedence

1. Define non-associative and right-associative infix operations analogous to infixl.

2. Add a constructor that puts parentheses around expressions to raise their precedence, but that is eliminated by a def definition. Test parsing with and without a pipe to pt -transform=compute.

Code generation as linearization

Translate arithmetic (infix) to JVM (postfix):

    2 + 3 * 4
  
      ===>
  
    iconst 2 : iconst 3 ; iconst 4 ; imul ; iadd

Just give linearization rules for JVM:

    lin
      EPlus  = postfix "iadd" ;
      EMinus = postfix "isub" ;
      ETimes = postfix "imul" ;
      EDiv   = postfix "idiv" ;
      EInt i = ss ("iconst" ++ i.s) ;
    oper
      postfix : Str -> SS -> SS -> SS = \op,x,y ->
        ss (x.s ++ ";" ++ y.s ++ ";" ++ op) ;

Programs with variables

A straight code programming language, with initializations and assignments:

    int x = 2 + 3 ;
    int y = x + 1 ;
    x = x + 9 * y ;

We define programs by the following constructors:

    fun
      PEmpty : Prog ;
      PInit  : Exp -> (Var -> Prog) -> Prog ;
      PAss   : Var -> Exp  -> Prog  -> Prog ;

PInit uses higher-order abstract syntax for making the initialized variable available in the continuation of the program.

The abstract syntax tree for the above code is

    PInit (EPlus (EInt 2) (EInt 3)) (\x ->
      PInit (EPlus (EVar x) (EInt 1)) (\y ->
        PAss x (EPlus (EVar x) (ETimes (EInt 9) (EVar y)))
          PEmpty))

No uninitialized variables are allowed - there are no constructors for Var! But we do have the rule

    fun EVar : Var -> Exp ;

The rest of the grammar is just the same as for arithmetic expressions here. The best way to implement it is perhaps by writing a module that extends the expression module. The most natural start category of the extension is Prog.

Exercises on code generation

1. Define a C-like concrete syntax of the straight-code language.

2. Extend the straight-code language to expressions of type float. To guarantee type safety, you can define a category Typ of types, and make Exp and Var dependent on Typ. Basic floating point expressions can be formed from literal of the built-in GF type Float. The arithmetic operations should be made polymorphic (as here).

3. Extend JVM generation to the straight-code language, using two more instructions

Thus the code for the example in the previous section is

    iconst 2 ; iconst 3 ; iadd ; istore x ;
    iload x ; iconst 1 ; iadd ; istore y ;
    iload x ; iconst 9 ; iload y ; imul ; iadd ; istore x ;

4. If you made the exercise of adding floating point numbers to the language, you can now cash out the main advantage of type checking for code generation: selecting type-correct JVM instructions. The floating point instructions are precisely the same as the integer one, except that the prefix is f instead of i, and that fconst takes floating point literals as arguments.

Lesson 7: Embedded grammars

Goals:

Functionalities of an embedded grammar format

GF grammars can be used as parts of programs written in other programming languages, to be called host languages. This facility is based on several components:

The portable grammar format

The portable format is called PGF, "Portable Grammar Format".

This format is produced by using GF as batch compiler, with the option -make, from the operative system shell:

    % gf -make SOURCE.gf

PGF is the recommended format in which final grammar products are distributed, because they are stripped from superfluous information and can be started and applied faster than sets of separate modules.

Application programmers have never any need to read or modify PGF files.

PGF thus plays the same role as machine code in general-purpose programming (or bytecode in Java).

Haskell: the EmbedAPI module

The Haskell API contains (among other things) the following types and functions:

    readPGF   :: FilePath -> IO PGF
  
    linearize :: PGF -> Language -> Tree -> String
    parse     :: PGF -> Language -> Category -> String -> [Tree]
  
    linearizeAll     :: PGF -> Tree -> [String]
    linearizeAllLang :: PGF -> Tree -> [(Language,String)]
  
    parseAll     :: PGF -> Category -> String -> [[Tree]]
    parseAllLang :: PGF -> Category -> String -> [(Language,[Tree])]
  
    languages    :: PGF -> [Language]
    categories   :: PGF -> [Category]
    startCat     :: PGF -> Category

This is the only module that needs to be imported in the Haskell application. It is available as a part of the GF distribution, in the file src/PGF.hs.

First application: a translator

Let us first build a stand-alone translator, which can translate in any multilingual grammar between any languages in the grammar.

  module Main where
  
  import PGF
  import System.Environment (getArgs)
  
  main :: IO ()
  main = do
    file:_ <- getArgs
    gr     <- readPGF file
    interact (translate gr)
  
  translate :: PGF -> String -> String
  translate gr s = case parseAllLang gr (startCat gr) s of
    (lg,t:_):_ -> unlines [linearize gr l t | l <- languages gr, l /= lg]
    _ -> "NO PARSE"

To run the translator, first compile it by

    % ghc -make -o trans Translator.hs

For this, you need the Haskell compiler GHC.

Producing PGF for the translator

Then produce a PGF file. For instance, the Food grammar set can be compiled as follows:

    % gf -make FoodEng.gf FoodIta.gf

This produces the file Food.pgf (its name comes from the abstract syntax).

The Haskell library function interact makes the trans program work like a Unix filter, which reads from standard input and writes to standard output. Therefore it can be a part of a pipe and read and write files. The simplest way to translate is to echo input to the program:

    % echo "this wine is delicious" | ./trans Food.pgf
    questo vino è delizioso

The result is given in all languages except the input language.

A translator loop

To avoid starting the translator over and over again: change interact in the main function to loop, defined as follows:

  loop :: (String -> String) -> IO ()
  loop trans = do
    s <- getLine
    if s == "quit" then putStrLn "bye" else do
      putStrLn $ trans s
      loop trans

The loop keeps on translating line by line until the input line is quit.

A question-answer system

The next application is also a translator, but it adds a transfer component - a function that transforms syntax trees.

The transfer function we use is one that computes a question into an answer.

The program accepts simple questions about arithmetic and answers "yes" or "no" in the language in which the question was made:

    Is 123 prime?
    No.
    77 est impair ?
    Oui.

We change the pure translator by giving the translate function the transfer as an extra argument:

    translate :: (Tree -> Tree) -> PGF -> String -> String

Ordinary translation as a special case where transfer is the identity function (id in Haskell).

To reply in the same language as the question:

    translate tr gr = case parseAllLang gr (startCat gr) s of
      (lg,t:_):_ -> linearize gr lg (tr t)
      _ -> "NO PARSE"

Abstract syntax of the query system

Input: abstract syntax judgements

  abstract Query = {
  
    flags startcat=Question ;
  
    cat
      Answer ; Question ; Object ;
  
    fun
      Even   : Object -> Question ;
      Odd    : Object -> Question ;
      Prime  : Object -> Question ;
      Number : Int -> Object ;
  
      Yes : Answer ;
      No  : Answer ;
  }

Exporting GF datatypes to Haskell

To make it easy to define a transfer function, we export the abstract syntax to a system of Haskell datatypes:

    % gf -make --output-format=haskell QueryEng.gf

The result is a file named Query.hs, containing a module named Query.

Output: Haskell definitions

  module Query where
  import PGF
  
  data GAnswer =
     GYes
   | GNo
  
  data GObject = GNumber GInt
  
  data GQuestion =
     GPrime GObject
   | GOdd GObject
   | GEven GObject
  
  newtype GInt = GInt Integer

All type and constructor names are prefixed with a G to prevent clashes.

The Haskell module name is the same as the abstract syntax name.

The question-answer function

Haskell's type checker guarantees that the functions are well-typed also with respect to GF.

  answer :: GQuestion -> GAnswer
  answer p = case p of
    GOdd x   -> test odd x
    GEven x  -> test even x
    GPrime x -> test prime x
  
  value :: GObject -> Int
  value e = case e of
    GNumber (GInt i) -> fromInteger i
  
  test :: (Int -> Bool) -> GObject -> GAnswer
  test f x = if f (value x) then GYes else GNo

Converting between Haskell and GF trees

The generated Haskell module also contains

  class Gf a where
    gf :: a -> Tree
    fg :: Tree -> a
  
  instance Gf GQuestion where
    gf (GEven x1) = DTr [] (AC (CId "Even")) [gf x1]
    gf (GOdd x1) = DTr [] (AC (CId "Odd")) [gf x1]
    gf (GPrime x1) = DTr [] (AC (CId "Prime")) [gf x1]
    fg t =
      case t of
        DTr [] (AC (CId "Even")) [x1] -> GEven (fg x1)
        DTr [] (AC (CId "Odd")) [x1] -> GOdd (fg x1)
        DTr [] (AC (CId "Prime")) [x1] -> GPrime (fg x1)
        _ -> error ("no Question " ++ show t)

For the programmer, it is enough to know:

Putting it all together: the transfer definition

  module TransferDef where
  
  import PGF (Tree)
  import Query   -- generated from GF
  
  transfer :: Tree -> Tree
  transfer = gf . answer . fg
  
  answer :: GQuestion -> GAnswer
  answer p = case p of
    GOdd x   -> test odd x
    GEven x  -> test even x
    GPrime x -> test prime x
  
  value :: GObject -> Int
  value e = case e of
    GNumber (GInt i) -> fromInteger i
  
  test :: (Int -> Bool) -> GObject -> GAnswer
  test f x = if f (value x) then GYes else GNo
  
  prime :: Int -> Bool
  prime x = elem x primes where
    primes = sieve [2 .. x]
    sieve (p:xs) = p : sieve [ n | n <- xs, n `mod` p > 0 ]
    sieve [] = []

Putting it all together: the Main module

Here is the complete code in the Haskell file TransferLoop.hs.

  module Main where
  
  import PGF
  import TransferDef (transfer)
  
  main :: IO ()
  main = do
    gr <- readPGF "Query.pgf"
    loop (translate transfer gr)
  
  loop :: (String -> String) -> IO ()
  loop trans = do
    s <- getLine
    if s == "quit" then putStrLn "bye" else do
      putStrLn $ trans s
      loop trans
  
  translate :: (Tree -> Tree) -> PGF -> String -> String
  translate tr gr s = case parseAllLang gr (startCat gr) s of
    (lg,t:_):_ -> linearize gr lg (tr t)
    _ -> "NO PARSE"

Putting it all together: the Makefile

To automate the production of the system, we write a Makefile as follows:

  all:
          gf -make --output-format=haskell QueryEng
          ghc --make -o ./math TransferLoop.hs
          strip math

(The empty segments starting the command lines in a Makefile must be tabs.) Now we can compile the whole system by just typing

    make

Then you can run it by typing

    ./math

Just to summarize, the source of the application consists of the following files:

    Makefile         -- a makefile
    Math.gf          -- abstract syntax
    Math???.gf       -- concrete syntaxes
    TransferDef.hs   -- definition of question-to-answer function
    TransferLoop.hs  -- Haskell Main module

Web server applications

PGF files can be used in web servers, for which there is a Haskell library included in src/server/. How to build a server for tasks like translators is explained in the README file in that directory.

One of the servers that can be readily built with the library (without any programming required) is fridge poetry magnets. It is an application that uses an incremental parser to suggest grammatically correct next words. Here is an example of its application to the Foods grammars.

JavaScript applications

JavaScript is a programming language that has interpreters built in in most web browsers. It is therefore usable for client side web programs, which can even be run without access to the internet. The following figure shows a JavaScript program compiled from GF grammars as run on an iPhone.

Compiling to JavaScript

JavaScript is one of the output formats of the GF batch compiler. Thus the following command generates a JavaScript file from two Food grammars.

    % gf -make --output-format=js FoodEng.gf FoodIta.gf

The name of the generated file is Food.js, derived from the top-most abstract syntax name. This file contains the multilingual grammar as a JavaScript object.

Using the JavaScript grammar

To perform parsing and linearization, the run-time library gflib.js is used. It is included in /src/runtime/javascript/, together with some other JavaScript and HTML files; these files can be used as templates for building applications.

An example of usage is translator.html, which is in fact initialized with a pointer to the Food grammar, so that it provides translation between the English and Italian grammars:

The grammar must have the name grammar.js. The abstract syntax and start category names in translator.html must match the ones in the grammar. With these changes, the translator works for any multilingual grammar.

Language models for speech recognition

The standard way of using GF in speech recognition is by building grammar-based language models.

GF supports several formats, including GSL, the formatused in the Nuance speech recognizer.

GSL is produced from GF by running gf with the flag --output-format=gsl.

Example: GSL generated from FoodsEng.gf.

    % gf -make --output-format=gsl FoodsEng.gf
    % more FoodsEng.gsl
  
    ;GSL2.0
    ; Nuance speech recognition grammar for FoodsEng
    ; Generated by GF
  
    .MAIN Phrase_cat
  
    Item_1 [("that" Kind_1) ("this" Kind_1)]
    Item_2 [("these" Kind_2) ("those" Kind_2)]
    Item_cat [Item_1 Item_2]
    Kind_1 ["cheese" "fish" "pizza" (Quality_1 Kind_1)
            "wine"]
    Kind_2 ["cheeses" "fish" "pizzas"
            (Quality_1 Kind_2) "wines"]
    Kind_cat [Kind_1 Kind_2]
    Phrase_1 [(Item_1 "is" Quality_1)
              (Item_2 "are" Quality_1)]
    Phrase_cat Phrase_1
  
    Quality_1 ["boring" "delicious" "expensive"
               "fresh" "italian" ("very" Quality_1) "warm"]
    Quality_cat Quality_1

More speech recognition grammar formats

Other formats available via the --output-format flag include:

Format

Description

gsl

Nuance GSL speech recognition grammar

jsgf

Java Speech Grammar Format (JSGF)

jsgf_sisr_old

JSGF with semantic tags in SISR WD 20030401 format

srgs_abnf

SRGS ABNF format

srgs_xml

SRGS XML format

srgs_xml_prob

SRGS XML format, with weights

slf

finite automaton in the HTK SLF format

slf_sub

finite automaton with sub-automata in HTK SLF

All currently available formats can be seen with gf --help.